Мен сәби кезімнен бастап, дәл қазірге дейін 70 жылдан астамтам уақыт өрнекті үйреніп те, үздіксіз машықтанып та және оны математикалық деңгейге дейін көтеріп зерттеп те келемін.
Осындай ұзақ уақыт үздіксіз құлшынуымның арқасында өрнектің бар тәжірибесін тереңдей анықтап, зерттеп, қыры мен сырын жете меңгердім. Оны былайша дәлелдеймін:
- «Өркениет өресіндегі қазақтың ою-өрнектері» атты төрт бөлім, он үш топ, отыз сегіз тарау, екі жүз алты тақырыппен өрнекті-математикалық деңгейдегі кітап жаздым.
- Бір парақ қағаз бетіне түсірген өрнекті бір гектар, тіпті одан да кең жазық бетке түсіре алатын болдым.
- Төкпе, жазба ақындар шабыты келгенде өлең шумақтарын бір-біріне ұқсатпай, төгіп-төгіп жіберетіні сияқты мен де математикалық деңгейдегі өрнекті бір-біріне ұқсатпай табан астында туындата салатын болдым.
Бұл арада «ғылым дегеніміз не?» деген сауалға мынадай ойымды білдіргім келеді. Әлемдегі болмыстың, яки қоғамдық, жаратылыстық бар саланың әрқайсысының тәжірибесін жан-жақты, жеріне жете тексеріп, зерттеп, нүктесін қалдырмай анықтап, қайта-қайтара сыннан өткізіп, тұрақтастырған, өзгермейтін, ешкім де өзгерте алмайтын етіп қорытындыланған заңды жүйені ғылым дейміз. Әрине, бұл менің жеке ойым.
Мен өрнекті осындай дәрежеде зерттеп кетпеген болармын. Дегенмен, «өрнек – ғылым» деген құпия пернесін ашып, саңылауын көрсеткендеймін. Өрелі ойдың иелері – зиялы қауым өз бағасын бере жатар. Бұл зерттеуімнен көп санаға ой туып, жан-жақты өрнек ғылымының құпиялығын ашып, толыққанды, кемелді өрнек ғылымының бар екенін түсінетініне сенемін.
Автордан
ӨРНЕККЕ ҚАТЫСТЫ ҒЫЛЫМИ АНЫҚТАМАЛАР
Қазақтың ою-өрнегі туралы
Қалыпты өмір кешкен қазақ ауылдарында қай үйге кірсеңіз де ою-өрнектер көзіңізден таса қалмайды. Тіпті дастарқан, басқа да бұйымдардың беттеріне, құрылыс нысандарына дейін қазақтың ою-өрнектері салынуда. Мұндай өрнектердің күрделісі де, жай қарапайымы да бар. Соңғы жылдары қазақтың ою-өрнектері реформаның бір табысы ретінде кішігірім фабрикалардың өндіріс салаларының қатарына енгізілуде. Алайда, қазақ ою-өрнектерінің нұсқасын ешқандай жобалау орындарының сызып бермегені анық. Мемлекеттік тоқыма фабрикаларында тоқылатын мата-кездемелердің гүл нұсқалары біртұтас жобаланып жатады. Оның жоба үлгісі мен басу технологиясы өз алдына бір жүйе. Ал қазақтың ою-өрнегі секілді ұлттық дәстүрлі өнімдер ол жүйеге әлі түсе қоймаған. Өнердің бұл аталы тәсілін қазірге дейін қазақ шеберлері дәстүрлік мұраларға сүйене отырып, бірден-бірге жалғастырушылар болуда. Бірақ, бұл қазақ өрнегінде ғылыми жүйе жоқ, я болмаса жай тәжірибелік өнер ғана деген сөз емес. Жазықтықтағы күрделі қисық сызықтардың тәртіпті, заңды, периодты жиынтығынан тұратын ою-өрнектер толық геометриялық жүйеге түседі. Мұны анықтау үшін біз төменде ою-өрнектерді геомеометриялық ережелер бойынша бөлшектеп, талдау жасаймыз, әрі геометриялық тәсілдермен қайта құрастырамыз.
Мұндағы геометриялық тәсілдерді жалпы орта мектепте оқыған жандар тегіс біледі. Ол түсінбейтін қиын да жүйе емес. Бұл тәсілдерді ғылыми негізде қолдану үшін, алдымен өрнектің негізгі бөлшектерін анықтаптануға қажетті математикалық, геометриялық анықтамаларға жүгінеміз.
Өстер туралы ұғымдар мен анықтамалар
Бәрімізге белгілі, қазақ ою-өрнектерінің негізгі бөлшектерінің бірі –қошқармүйіздер. Олар әр алуан мүйіздермен салынады. Мысалы, «қошқармүйіз», «сыңар мүйіз», «қос мүйіз», «сынық мүйіз» дегендердің бәрі әр түрлі радиустағы шеңбер доғаларының ұштастырылуы болып саналады. Мұны анықтау үшін бізге «сан өсі» ең бірінші геометриялық құрал болады.
Сан өсі, координата жүйесі және симметрия өсі
Жазықтықтан қағаз бетіне бір түзу салып, оның қолдануға қолайлы болуы үшін қағаз шетіне параллель сызып, оған солдан оңға қараған өс бағытын және қақ ортасынан өстің басын – О нүктесін белгілесек, содан соң өлшемді сызғышпен тең бірліктерге бөліп шықсақ, бұл сан өсі болып шығады.
Сан өсі көріністе жай бір сызық болып көрінгенімен, оның өстік басын «О» нүктесінің екі жағына барлық нақты сандарға (оң, теріс) бірдей жатқызуға болады. Демек, оған алынатын бірлік шексіз. Дегенмен, өрнек сызуда қолайлы болуы үшін, әдетте, сантиметрді бірлік етіп аламыз.
Біз жазықтыққа сан өсін сызғанда, оның өсі жазықтықты, дәлірек айтқанда, қағаздың бетін екіге бөліп тұрғанын көреміз. Бұл екі бөліктің бірін А, екіншісін В деп белгілейік.
Жоғарыдағы қарапайым бір сызықпен-ақ біз осы жазықтыққа едәуір күрделі сызулар сызудың шартын әзірледік. Мысалы, циркульді алып, белгілі нүктені центр етіп айналдырсақ, шеңбер сызылады. Түрлі радиус пен бір центрден сансыз коцентрлі шеңберлер, бір түрлі радиус пен центрін өсті бойлай жылжыта отырып сансыз жылжыма шеңберлер, т.б. сызып шыға аламыз.
Біз жоғарыда бірден ауызға алған «қошқармүйіз» дегеніміз, шындығында, осы шеңберлердің белгілі бір формада ұштасуы. Оған төменде арнайы тоқталамыз.
Мұнан басқа да қазақтың ою-өрнектерінде кезігетін айшықтар да әлгінде көрсетілген параллель жылжыған шеңберлердің қиылыстырмасынан түзіледі. Оған да өз кезегінде арнаулы орын береміз. Қысқасы, өс бағыты, бас нүктесі және ұзындық бірлігі деп аталатын үш фактордан құралған сан өсінің бойынан сан түрлі өрнекке негіз шығарып ала аламыз.
Төменде біз сан өсі бойынан ою-өрнек бөлшектерін сызудың нақты мысалдарын қарап өтеміз. Ою-өрнектегі қисық сызықтар – бұлар анықталмаған фигуралар. Ендеше, қошқармүйізді қисық сызықтың ғылымилығына тоқталайық.
Жазықтықтағы тікбұрышты координата
Жазықтықта қолайлы орыннан таңдап алынған «О» нүктесінен бір-біріне перпендикуляр жүргізілген бірі координатал (жаттық), бірі вертикаль (тік), екіншісі – вектор (бағытты кесінді) координата деп аталады. Координатал өс – абсцисса, вертикаль өс – ордината болады. Абсциссаны әдетте Х деп, ал орбитаны У-пен таңбалаймыз. Біз жайшылықта бұл атауларға тым таңданып отырмай-ақ, алдымыздағы бір бет қағазды ұзынынан бір, көлденеңінен бір бүктесек болғаны, бір координата жүйесі шығады. Сонда мұның көлденең (тура) сызығы абсцисса (ендік өс), тік сызығы ордината (бойлық өс) болады. Бұл екі өстің өлшемдері ұқсас алынады. Өстердің бөлуден кейінгі төрт бөлігін оңнан солға қарай ретімен І, ІІ, ІІІ, ІV ширектер деп аламыз (2 А-сурет).
Координата деген сөз латынның Со – бірге, ordinatus – реттелген, анықтау деген сөзінен алынған. Демек, нүктенің орнын қосақтап анықтау болып шығады. Мысалы, берілген А нүктесінің абсциссасы 1, ординатасы 3 болса, В нүктесінің абсциссасы – 2, ординатасы 4 болса, онда А (1,3), В (– 2,4) деп жазылады (2 В-сурет).
Орта мектептік білімі бар адамдар нүкте орнының анықталуына қоса, координаталар үстінен анықталған қисық сызықтардың графиктерін де сыза алады. Белгілі қисық сызықтың формуласы берілгеннен кейін, сол бойынша оның бірнеше нүктесінің орнын тауып, оларды жалғастырсақ, сол қисық сызықтың графигі шығады.
Координаталар жүйесінде ою-өрнектер сызудағы ең жарамды құрал болатын жері – жалаң график (өрнек) сызумен ғана шектелмейді. Бұдан да маңыздысы – бір ширекке түскен бөлшек өрнекті екінші бір ширекке мүлтіксіз көшіру оңай әрі нақты шартты әзірлеп береді. Мұны өрнектерді құрастыру мазмұнында анықтап айтатын боламыз.
Ою-өрнекке қатысты жиі қолданылатын симметрия туралы анықтамалар
Табиғатта, техникада және тұрмыста кейбір денелердің бөліктері өзара ұқсас, үйлесімді орналасады. Жәндіктерді, ою-өрнектерді, бұйымдарды, т.б. (3-А; В; С-суреттер) мысалға келтірсек болады.
Мұндай жағдайда, дененің, фигураның бөліктері симметриялы деген сөздерді жиі кездестіреміз. «Симметрия» грек сөзінен алынған, ол «үйлесім» сөзі сияқты, бірдей өлшемділікте, белгілі бір реттілікпен орналасқан деген ұғымды білдіреді.
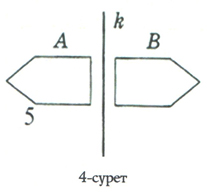
Симметрия әр түрлі болады. Симметрияның ең қарапайым түрі – түзуге қатысты симметрия. Мысалы, 4-суретте көрсетілген жазықтықтағы А фигурасы В фигурасына r түзуіне қатысты симметриялы орналасқан.
Кез келген геометриялық фигура нүктелерден құралатындықтан, түзуге қатысты симметриялы нүктелерді салуды үйренейік. Мысалы, r түзуіне қатысты А нүктесіне симметриялы А1 нүктесін салайық (5-сурет).
Ол үшін r түзуін сызып, одан тыс жатқан А нүктесін белгілеу керек;
А нүктесі арқылы r түзуіне перпендикуляр түзу жүргіземіз: AD^r;
Перпендикулярдың r түзуінен кейінгі созындысына D нүктесінен бастап ұзындығы AD-ға тең DА1 кесіндісін саламыз. Сонда r түзуіне қатысты А нүктесіне симметриялы А1 нүктесі пайда болады.
Симметриялы екі нүкте бірдей әріппен белгіленіп, тек олардың біреуінің төменгі оң жақ ұшына цифр-индекс қойылады.
Түзуге қатысты берілген кесіндіге симметриялы кесіндіні салуды қарастырайық. Мысалы, s түзуіне қатысты АВ кесіндісіне симметриялы А1В1 кесіндісін салу үшін (6-сурет):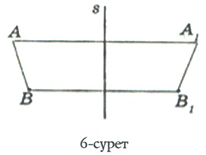
АВ кесіндісінің А және В нүктелеріне s түзуіне қатысты симметриялы А1 және В1 гүктелерін салу керек.
А1 және В1 нүктелерін қосып, А1В1 кесіндісін аламыз.
S түзуіне қатысты АВ кесіндісіне А1В1 кесіндісі симметриялы болады. Егер s түзуі бойымен жазықтықты бүктесек, АВ түзуі А1В1 түзуімен беттеседі. Демек, АВ=А1В1.
Егер түзудің бойымен бүктегенде жазықтықтағы екі фигура бір-бірімен беттесетін болса, ондай фигуралар түзуге қатысты симметриялы фигуралар деп аталады.
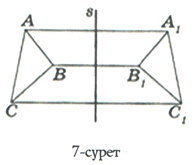
7-суретте s түзуіне қатысты симметриялы ұшбұрыштар кескінделген.
Мұндағы D АВС =D А1В1С1
Себебі жазықтықты s түзуінің бойымен бүктесек, олардың сәйкес төбелері (А төбесі А1 төбесімен, В төбесі В1 төбесімен, С төбесі С1 төбесімен) беттеседі.
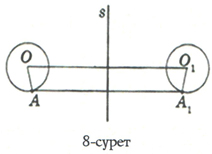
8-суреттегі центр О нүктесі, радиусы ОА кесіндісі болатын шеңбер центрі О1 нүктесі, радиусы О1А1 болатын шеңбермен s түзуіне қатысты симметриялы болады.
Симметриялы фигуралар өзара тең деп саналады.
Егер фигураны симметриялы екі бөлікке бөлсек, мұнда ондай фигура өстік симметриялы фигура деп аталады. Түзу сол фигураның симметрия өсі деп аталады.
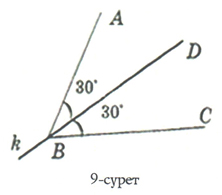
Мысалы, 9-суреттегі АВС бұрышының АВ қабырғасы r түзуіне қатысты ВС қабырғасына симметриялы. Демек, бұрыш – өстік симметриялы фигура.
<АВС=60°. АВС бұрышын r түзуі бойымен бүктесек, ол градустық өлшемдері тең екі бұрышқа бөлінеді. Сонда r түзуі АВС бұрышының симметриялы өсі болады. Бұрыштың симметриялы осі оның биссектрисасы болып есептеледі.
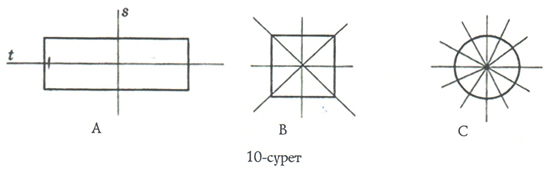
Тік төртбұрышты, квадратты, шеңберді – өстік симметриялы фигуралар (10, А, В, С-суреттер) деп атаймыз.
Тік төртбұрыштың екі симметриялы осі бар, квадраттың төрт симметриялы осі бар. Шеңбердің кез келген диаметрі арқылы өтетін түзу оның радиусы болмақ.
Симметрияның екінші түрі – нүктеге қатысты симметриялы дейміз.
О нүктесіне қатысты А нүктесіне симметриялы А1 нүктесін салуды үйренейік.
Ол үшін: 1)А және О нүктелерін белгілеп, осы нүктелері арқылы r түзуін жүргізейік.
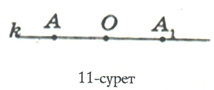
2) Түзудің бойында ОА кесіндісіне тең ОА1 кесіндісін өлшеп салу керек: ОА=ОА1 (11-сурет).
Мұндағы А және А1 нүктелері О нүктесіне қатысты симметриялы нүктелер болады.
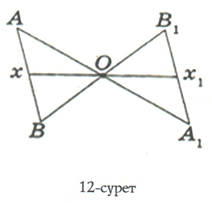
О нүктесіне қатысты АВ кесіндісіне симметриялы кесінді салуды үйренейік (12-сурет).
Ол үшін: 1) О нүктесіне қатысты А нүктесіне симметриялы А1 нүктесін В нүктесіне симметриялы В1 нүктесін салайық.
2) А1 және В1 нүктелерін қоссақ, А1В1 кесіндісі алынады. АВ және А1В1 кесінділері О нүктесіне қатысты симметриялы. А1В1 кесіндісіндегі қандай да бір х1 нүктесі О нүктесіне қатысты АВ кесіндісіндегі х нүктесіне симметриялы болып шығады.
Егер О нүктесінен АВ кесіндісін 180°-қа бұрсақ, ол А1В1 кесіндісімен беттеседі. Демек, АВ кесіндісіне симметриялы А1В1 кесіндісін салу үшін АВ кесіндісін О нүктесінен 180°-қа бұру да жеткілікті дейміз.
О нүктесіне қатысты АВС ұшбұрышына симметриялы А1В1С1 ұшбұрышын салу үшін: О нүктесіне 
қатысты А,В, және С нүктелеріне симметриялы А1, В1 және С1 нүктелерін салып, оларды кесінділермен қоссақ жеткілікті (13-сурет) болады.
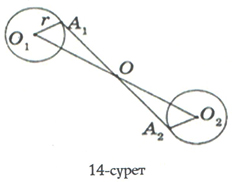
О нүктесіне қатысты центрі О1 радиусы А1О1= r шеңберіне симметриялы шеңбер салайық (14-сурет).
Ол үшін: 1) Берілген щеңбердің центрі О1 нүктесіне О нүктесіне қатысты симметриялы О2 нүктесін салу керек;
2) Берілген шеңбердің радиусы А1О1 кесіндісіне О нүктесіне қатысты симметриялы А2О2 кесіндісін саламыз;
3) Центрі О2 нүктесі, радиусы А2О2 шеңберін жүргізу керек. О нүктесіне қатысты центрі О2, радиусы А2О2 болатын шеңбер центрі О1, радиусы А1О1 болатын шеңберге симметриялы деп білеміз.
Егер О нүктесіне қатысты симметриялы нүктелер фигураның өзінде жатса, ол фигура центрлік симметриялық фигура деп аталады.
О нүктесі фигураның симметриялы центрі болып шығады.
Мысалы, шеңбердің қандай да бір диаметрінің бойындағы нүктелері оның центріне қатысты симметриялы (15-сурет) болмақ.
О нүктесіне (симметрия центріне) қатысты Х нүктесі Х1 нүктесіне, Ү нүктесі Ү1 нүктесіне, Z нүктесі Z1 нүктесіне, т.с.с. симметриялы болады.
Шеңбер – центрлік симметриялы фигура
Шеңбердің симметрия центрі – шеңбердің центрі болатын О нүктесі.
Кесінді – центрлік симметриялы фигура (16-сурет) болып есептеледі.
Кесіндіні тең екі бөлікке бөлетін (АО-ОВ) О нүктесі – оның симметриялы центрі деп танылады.
Тік төртбұрыш – центрлік симметриялы фигура
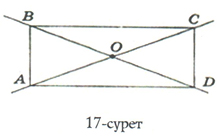Тік төртбұрыштың қарама-қарсы төбелерін қосатын кесінді диагональ деп аталады (17-сурет). АС және ВD кесінділері – диагональдар деп аталады.
Тік төртбұрыштың диагональдарының қиылысу нүктесі – оның симметриялы центрі деп аталады. О нүктесі – АВСD тік төртбұрышының симметриялы центрі болады.
Тік төртбұрыштың О симметрия центріне қатысты А төбесі С төбесіне, В төбесі D төбесіне симметриялы. Сондықтан: АО = ОС: ВО = ОD.
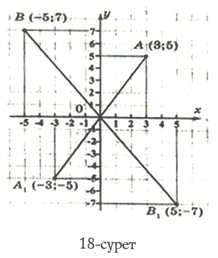Координаталық жазықтықтағы координаталардың басы О нүктесіне қатысты центрлік симметриялы нүктелерді қарастырайық (18-сурет).
Координаталық жазықтықтағы координаталардың басы О нүктесіне қатысты А (3;5) нүктесіне А1 (– 3; – 5) нүктесіне және В (– 5; 7) нүктесі В1 (5; – 7) нүктесіне симметриялы орналасқан.
Координаталық жызықтықтағы координаталардың басы О нүктесіне қатысты симметриялы нүктелердің координаталары қарама-қарсы сандар болады.
Болатбай НӘСІЛБЕКҰЛЫ
(Басы. Жалғасы бар)
